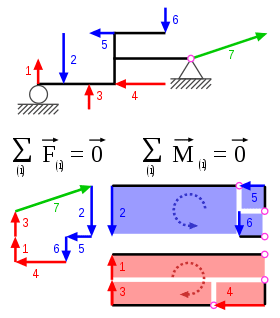
Las estructuras se pueden clasificar estáticamente en función de su grado de indeterminación estática, bajo esta premisa en este blog se tratará de clasificarlas y explicar cada uno de estos tipos.
Partamos de lo más básico sobre lo que conocemos en estructuras y la estática: «Toda estructura debe cumplir con las condiciones que se derivan de las tres componentes que intervienen en su cálculo (estática, cinemática y leyes del comportamiento)«, las mismas que se traducen en las ecuaciones de equilibrio, ecuaciones de compatibilidad y ecuaciones constitutivas.
Ahora bien, calcular una estructura implica determinar las variables estáticas que esta posee: Reacciones, esfuerzos y cargas; es por ello que antes de abordar algún cálculo sobre la estructura, debemos determinar su número o grado de indeterminación estática con el fin de abordar el mejor método adecuado para su resolución estática en función a su clasificación.
Grado de Indeterminación Estática
El Grado de Indeterminación Estática (GIE) o Grado de Hiperestaticidad es el número de fuerzas redundantes de la estructura, es decir, el número de incógnitas independientes que no pueden determinarse mediante las ecuaciones de equilibrio de la estructura, dado que el número de incógnitas estáticas excede el número total de ecuaciones de equilibrio disponibles.
El número de fuerzas redundantes no varía para una misma estructura, aunque si variará la selección que se haga de éstas de entre todas las fuerzas incógnitas.
Para comenzar, llamaremos a las variables de las siguientes maneras:
- B = número de barras
- N = número de nudos
- ΣDtb = número de desconexiones totales en extremos de barra
- ΣR = número de reacciones
El número total de incógnitas estáticas se obtiene sumando las incógnitas externas (reacciones) y las incógnitas internas (esfuerzos de extremo de barra). Dado que una barra perteneciente a una estructura plata tiene 2 extremos (i, j) y 3 esfuerzos en cada una de ellas (axial, cortantes y flector: Fxi, Fyi, Mi, Fxj, Fyj, Mj), entonces el número total de incógnitas estáticas será:
Número total de incógnitas estáticas: 6B + ΣR
El número total de ecuaciones de equilibrio se obtiene sumando las ecuaciones de equilibrio en nudo y en barra, que son 3 respectivamente en el caso de estructuras planas. A estas hay que sumarle una ecuación por cada desconexión total en extremo de barra, ya que aporta una condición de esfuerzo nulo en la dirección de la desconexión.
Número total de ecuaciones en equilibrio: 3N + 3B + ΣDtb
El GIE se obtiene descontando del numero total de incógnitas estáticas el número de ecuaciones de equilibrio, es decir, mediante la expresión:
GIE = (6B + ΣR) – (3N + 3B + ΣDtb) = (3B + ΣR) – (3N + ΣDtb)
La aplicación de esta expresión implica una modelización previa de la estructura, separando nudos y barras y asignando a cada extremo de éstas sus condiciones de vínculo, así como identificando los tipos de apoyo y sus reacciones asociadas.
Pude utilizarse una variante de esta expresión que no necesita modelización si se distingue entre nudos libres (NL) y apoyos (A) y se añaden las desconexiones totales en los apoyos (Dta), entonces:
3N = 3NL + 3A y ΣR= 3A – ΣDta
Al sustituir en la expresión del GIE se obtiene esta nueva expresión que no necesita de modelización previa:
GIE = (3B + ΣR) – (3N + ΣDtb) = (3B + 3A + ΣDta) – (3NL + 3A + ΣDtb)
GIE = (3B) – (3NL + ΣDtb + ΣDta)
Ahora miremos un ejemplo:
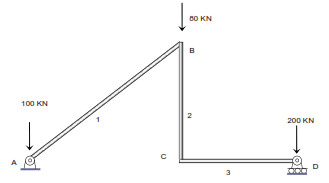
B = 3 (barras 1, 2 y 3)
NL = 2 (Nudos B y C)
A = 2 (Apoyos A y D)
ΣDtb = 0 (No hay desconexiones entre barras, los nudos B y C son rígidos)
ΣDta = 3 (Giro en A, movimiento horizontal y giro en D)
Por tanto: GIE = (3B) – (3NL + ΣDtb + ΣDta) = 9 – (6 + 0 + 3) ➡ GIE = 0
Calcularemos ahora el GIE de la misma estructura a partir de la modelización representada en la siguiente figura, en la que se ha asociado la rótula al extremo i de la barra 1 y el carrito al extremo j de la barra 2:
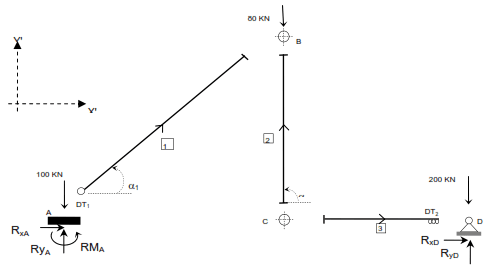
Según esta modelización:
B = 3 (barras 1, 2 y 3)
N = 2 (Nudos B y C)
A = 4 (2 nudos libres, B y C, y 2 apoyos A y D))
ΣDtb = 2
ΣR = 5 (tres en A y 2 en D)
Por tanto: GIE = (3B + ΣR) – (3N + ΣDtb) = (9 + 5) – (12 + 2) ➡ GIE = 0
Clasificación de las estructuras
Las estructuras se clarifican estáticamente según su GIE en:
- Estructuras Isostáticas: GIE = 0
- Estructuras Hiperestáticas: GIE > 0
- Estructuras hipostáticas: GIE < 0
Estructuras Isostáticas
Una estructura es isostática es cuando el GIE = 0. En ese caso el número de ecuaciones de equilibrio coinciden con el número de incógnitas.
Una estructura isostática tiene una única configuración estática admisible y está estáticamente determinada. Se obtiene aplicando solo las ecuaciones del equilibrio.
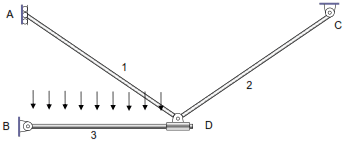
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 9 – (3 + 3 + 3) = 0
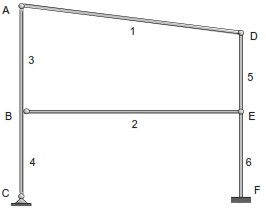
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 18 – (12 + 5 + 1) = 0
Estructuras Hiperestáticas
Una estructura es hiperestática cuando el GIE > 0. En ese caso el número de ecuaciones de equilibrio es menor al número de incógnitas estáticas.
Una estructura hiperestática tiene infinitas configuraciones estáticamente admisibles. Será, por lo tanto, estáticamente indeterminada.
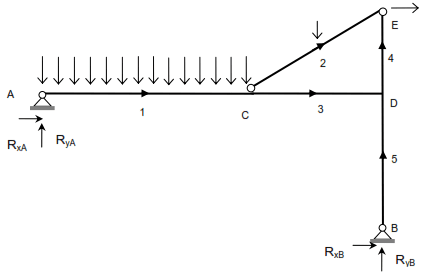
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 15 – (9 + 2 + 2) = 2
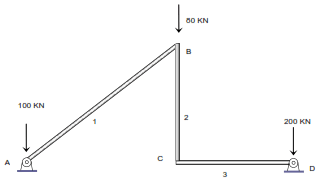
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 9 – (6 + 0 + 2) = 1
Estructuras Hipostáticas
Una estructura es hipostática cuando el GIE < 0. En ese caso el número de ecuaciones de equilibrio es excesivo ya que supera el número de incógnitas estáticas. Se trata de un mecanismo, es decir, una estructura inestable que no puede equilibrarse.
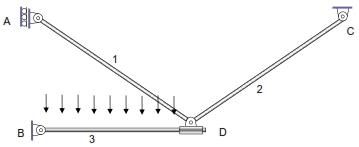
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 9 – (3 + 3 + 4) = -1
Pero el hecho de que el GIE sea igual o mayor que 0 no garantiza que la estructura sea estable, pudiendo tener una estabilidad local y, por tanto, será un mecanismo.
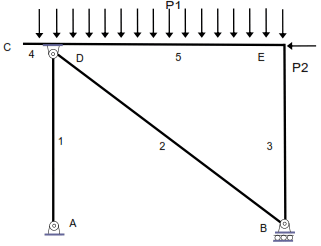
GIE = (3B) – (3NL + ΣDtb + ΣDta) = 15 – (9 + 2 + 4) = 0
El valor del GIE es 0, luego podría suponerse que la estructura es isostática, sin embargo, no lo es. La estructura no puede equilibrarse horizontalmente. La barra 1 es biarticulada y no tener cargas perpendiculares a su directriz tendrá cortante nulo, es decir, la reacción horizontal en A es nula.
Como en B el movimiento horizontal está permitido, no hay reacción. La fuerza horizontal P2 no puede equilibrarse. Si rigidizáramos la unión entre la barra 2 y la viga (4-5), dejando únicamente articulado el soporte 1, obtendríamos un GIE de valor 1, sin embargo, la estructura seguiría sin poder equilibrarse a fuerzas horizontales.
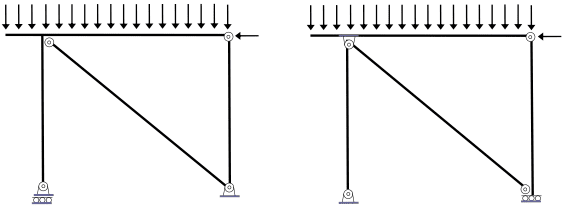
Se proponen entonces estos 2 ejemplos para determinar el GIE y para verificar si se trata de mecanismos o no. En ambos casos el GIE es 0 pero solo la estructura de la izquierda es isostática, y la de la derecha es un mecanismo.
En este blog se tratado de definir que es el grado de indeterminación estática de una estructura y como obtener este valor, posteriormente se han clasificado las estructuras en función de este planteándose algunos ejemplos interactivos. ¡No te olvides de compartir este blog si te resultó útil, a otras personas también les puede ayudar 👌!
👇 Me puedes encontrar en las siguientes redes sociales 👇
Si deseas adquirir las más de 30 carpetas que tenemos en la MEGA (ojo, son de pago), puedes contactarte conmigo dando clic al botón de abajo 👇