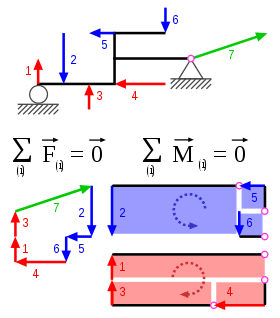
¿Qué es?
Desarrollado por Christian Otto Mohr (1835 – 1918), el círculo de Mohr es un método gráfico para determinar el estado tensiones en los distintos puntos de un cuerpo.
Este método gráfico es utilizado para encontrar las principales tensiones y las tensiones normales en varios planos. Cada punto de la circunferencia del círculo de Mohr representa un cierto plano que da el valor de la tensión normal y la tensión cortantes en ese plano.
Esta herramienta gráfica comúnmente utilizada por los ingenieros para analizar gráficamente las tensiones de corte principales y máximas en cualquier plano.
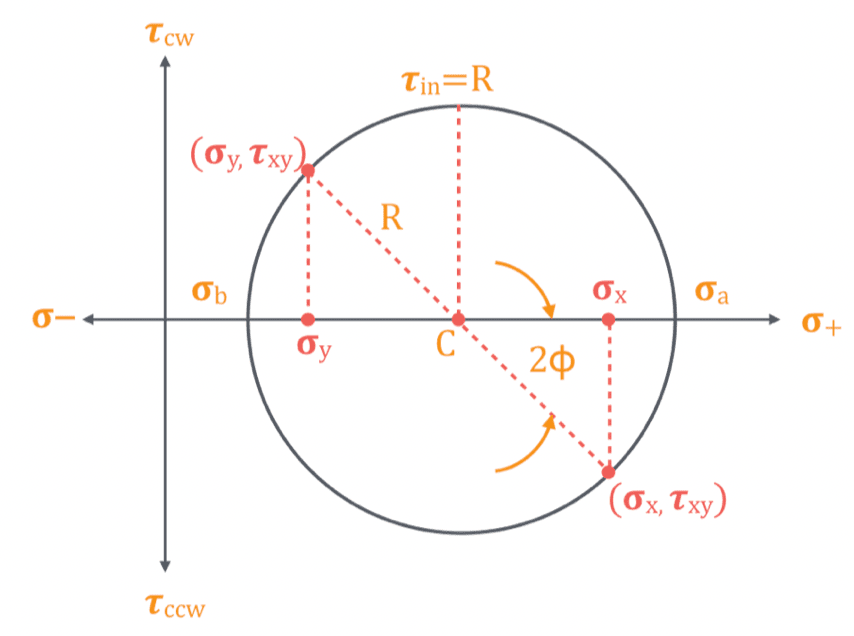
El plano principal o plano principal máximo es el plano en el que el valor de la tensión normal está en un punto MÁXIMO, y este valor se conoce como tensión principal máxima.
Del mismo modo, habrá un plano más, conocido como plano principal mínimo, en el que el valor de tensión normal es mínimo, y este valor se denominará estrés principal mínimo.
A continuación se muestra un elemento sometido a estrés típico en 2D con todos sus componentes en sentido positivo:
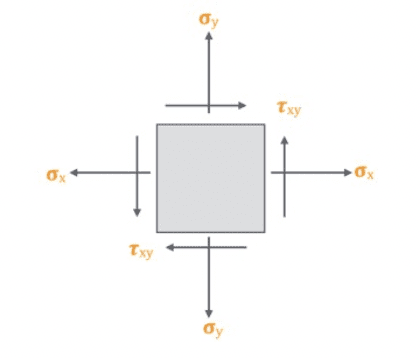
Teoría del círculo de Mohr en 2D
Considere un cuerpo sobre el cuál actúa un estado plano de cargas. Consideremos al plano de carga para nuestro sistema al plano xy:
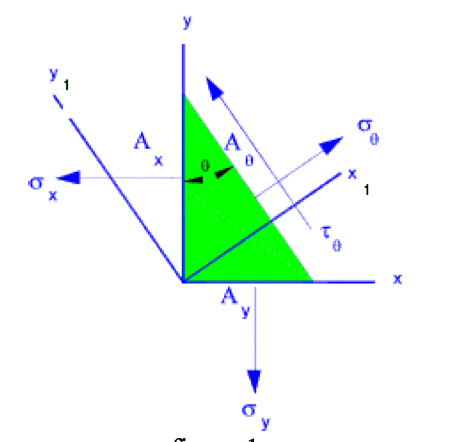
De modo que no existan esfuerzos en el sentido perpendicular a este (esfuerzos en z nulos). Adoptamos un elemento triangular donde se supone que los ejes x e y son principales, o sea las tensiones de corte en esos planos son nulas.
Esta suposición se hace con el fin de no complicar por demás la matemática siendo el objeto de este desarrollo conocer el desarrollo matemático a fin de ser asociado con el Mode físico.
Del Plano xy, además de los ejes x e y, se muestra otro par de ejes coordenados los cuales han sido rotados a un ángulo ⍬ respecto del eje z (normal al plano), el par de ejes x1 e y1 son normal y tangente al plano A⍬ respectivamente.
Queremos obtener una relación entre las tensiones en las áreas Ax, Ay y A⍬. Evaluaremos el equilibrio de fuerzas en la dirección del eje x:

Ahora evaluemos el equilibrio de fuerzas en la dirección del eje y:

Considerando que Ax = A⍬cos⍬ y que Ay = A⍬sen⍬, reemplazamos las ecuaciones 1 y 2:
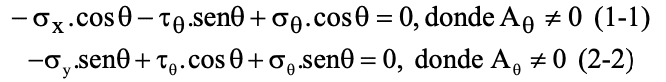
Multiplicando la ecuación 1 por cos⍬, la 2 por sen⍬ y sumando ambas se llega a:

Y considerando las relaciones trigonométricas:
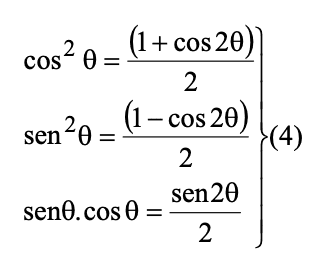
Se llega a:
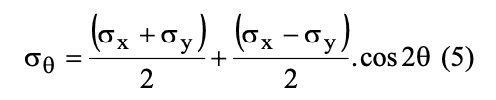
Analizamos las ecuaciones 1 y la 2 para obtener el corte en el plano ⍬: Multiplicando la ecuación 1 por ser⍬, la 2 por cos⍬, sumando ambas y considerando las relaciones trigonométricas 4 se llega a:

Obsérvese que las ecuaciones 5 y 6 no son más que las componentes cartesianas de los puntos correspondientes a una circunferencia en el plano xy, la ecuación de la circunferencia se obtiene considerando la relación trigonométrica:

Entonces reemplazando en 5 y 6 se obtiene:
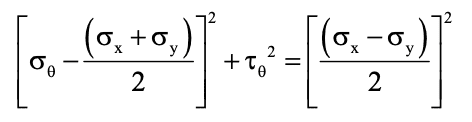
Esta circunferencia es lo que denominamos «Círculo de Mohr» para dos dimensiones. En esta circunferencia el ángulo formado por la recta con origen en el centro de la misma:
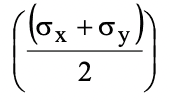
Y un punto cualquiera perteneciente al perímetro de la circunferencia, tiene valor de 2⍬, siendo ⍬ el ángulo de inclinación del plano para el cuál las tensiones sobre esa superficie valen σθ y τθ. Consideremos σx< σy.
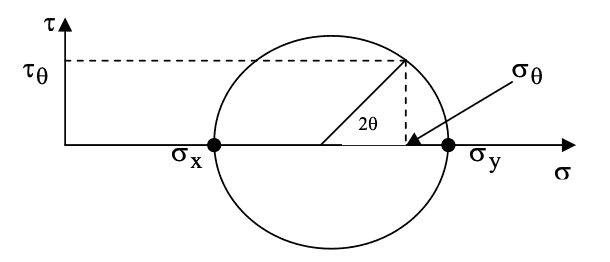
Así como se calculó el estado tensiones en el plano θ a partir de las tensiones principales, el proceso se puede hacer de manera inversa. Conociendo el estado de carga para una cierta terna de ejes se pueden conocer las tensiones principales de un sistema dado.
Usos del círculo de Mohr
- Al dibujar un solo círculo de Mohr, podemos encontrar fácilmente tensiones normales y tangenciales en varios planos oblicuos inclinados, lo que es difícil utilizando el método analítico.
- Mediante el uso del círculo de Mohr, es fácil calcular las tensiones principales, la tensión de corte máxima, la tensión resultante, el ángulo del plano principal, etc.
- El método del círculo de Mohr es un método simple y rápido que el método analítico.
Datos importantes sobre el círculo de Mohr
- Las tensiones normales se trazan a lo largo de la abscisa. Las tensiones de tracción se consideran positivas y las tensiones de compresión se consideran negativas.
- La tensión de corte se traza como ordenada. La tensión de corte que causa la rotación del elemento en el sentido de las agujas del reloj se considera positiva, mientras que otra que causa rotación en sentido contrario a las agujas del reloj se considera negativa.
- Las coordenadas de varios puntos del círculo de Mohr representan el estado de estrés de diferentes planos.
- El radio del círculo a cualquier punto de su circunferencia representa el eje dirigido normal al plano cuyos componentes de tensión están dados por las coordenadas de ese punto.
- El ángulo entre los radios y los puntos del círculo de Mohr es el doble del ángulo entre las normales y los planos reales representados por estos puntos. El sentido de rotación de este ángulo es el mismo que el sentido de rotación del ángulo real entre las normales y el plano.
Ejemplo práctico de Círculo de Mohr
Ejemplo a continuación sin valores numéricos del análisis mediante el Círculo de Mohr. sea una viga empotrada con presión interna, momento torso y una carga P aplicada en el extremo libre.

Sección:

Se desea conocer el tenor de tensiones para ciertos puntos del sistema dado, según el estado de cargas. El tensor de tensiones de la forma:
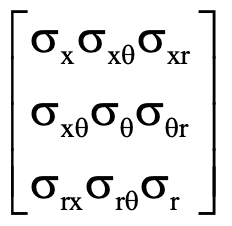

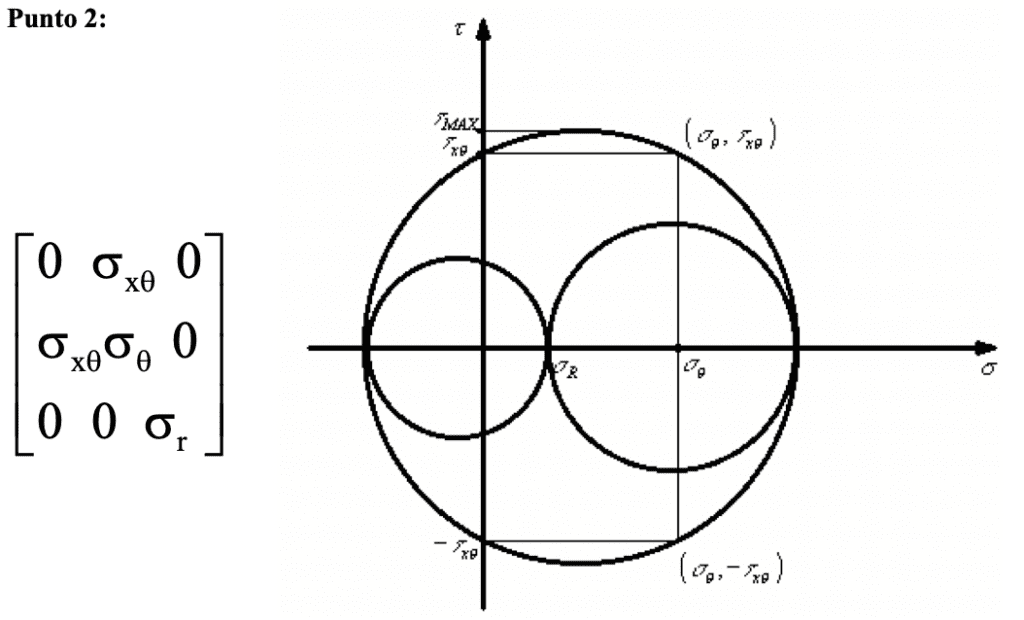
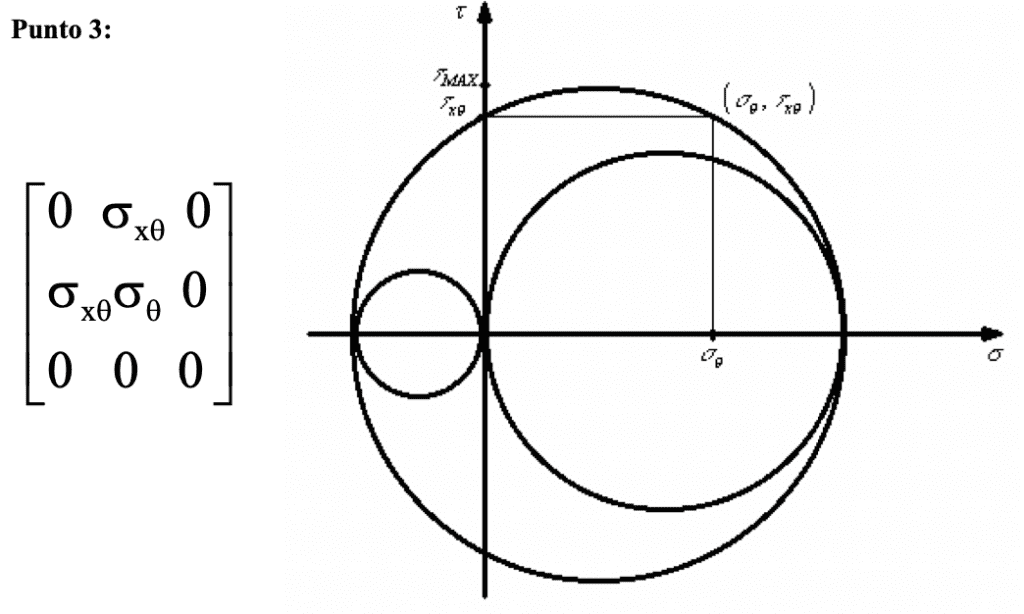
Cabe destacar que tanto en el punto 1, como el 2, la tensión de corte esta dada por el Momento Torsor. En cambio para el punto 3, la tensión de corte esta dada por el Momento Torsor y la Carga aplicada en el extremo libre,
También se observa que en todos los puntos analizados la tensión σR es principal.
🔧 ¿Quieres profundizar en la ingeniería? Descubre «El Glosario del Ingeniero» 📘
Si estás buscando ampliar tus conocimientos en el mundo de la ingeniería, ¡nuestro E-Book «El Glosario del Ingeniero» es tu aliado perfecto! Con una colección exhaustiva de conceptos, definiciones y ejemplos, este libro electrónico te llevará a un viaje de aprendizaje inigualable.

¡No te olvides de visitar mis redes sociales!