Los diagramas de fuerza cortante y momento flector son métodos gráficos potentes que se utilizan para analizar una viga bajo una carga (puntual, distribuida, etc.).
En este artículo trataré de explicarte qué son las fuerzas cortantes y los momentos flectores, por qué son útiles, enserio lo son!, así como el procedimiento para dibujar los diagramas y también algunos otros aspectos clave utilizados en estructuras.
¿Qué son las fuerzas cortantes y los momentos flectores?
Cuando se aplican cargas a una viga, se desarrollan fuerzas internas dentro de la viga en respuesta a las cargas. Podemos visualizar estas fuerzas haciendo un corte imaginario a través de la viga y considerando las fuerzas internas que actúan sobre la sección transversal. Estas fuerzas internas tienen dos componentes:
- Fuerzas cortantes , que están orientadas en dirección vertical, paralelas a la sección transversal de la viga.
- Fuerzas normales , que están orientadas a lo largo del eje de la viga, perpendicular a la sección transversal de la viga.
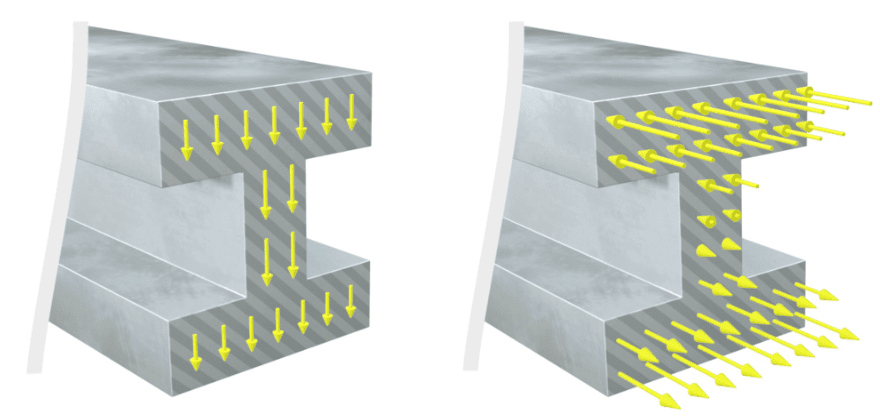
Las fuerzas internas se desarrollan de tal manera que se mantiene en equilibrio. No importa dónde se realice el corte imaginario a lo largo de la viga, el efecto de las fuerzas internas siempre equilibrará el efecto de las fuerzas externas.
Las tensiones normales serán de tracción en un lado de la sección transversal y de compresión en el otro. Si la viga está flexionada, la parte superior de la viga se acortará y, por lo tanto, las fuerzas normales que actúan en la parte superior serán de compresión. La parte inferior de la viga se alargará y, por lo tanto, las fuerzas normales que actúan en la parte inferior de la viga serán de tracción.

Estas fuerzas se cancelan entre sí, por lo que no producen una fuerza neta perpendicular a la sección transversal de la viga, pero sí producen un momento.
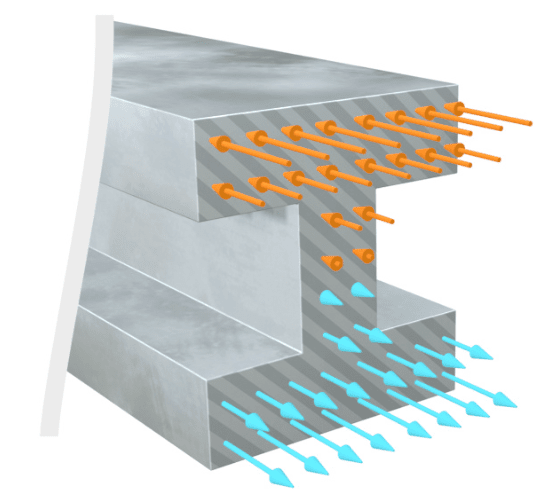
Esto significa que las fuerzas internas que actúan sobre la sección transversal de la viga se pueden representar mediante una fuerza resultante, llamada «Fuerza Cortante», que es la resultante de las fuerzas cortantes internas, y por un momento resultante, llamado «Momento flector», que es la resultante de las fuerzas normales internas.

¿Por qué son útiles los diagramas de fuerza cortante y momento flector?
Los diagramas de fuerza cortante y momento flector se utilizan para analizar y diseñar vigas. Al mostrar cómo varían la fuerza cortante y el momento flector a lo largo de una viga, permiten cuantificar la carga sobre la viga.
A menudo se utilizan como punto de partida para realizar análisis más detallados, que pueden incluir el cálculo de tensiones en las vigas o la determinación de cómo se deformarán las vigas.
Cargas y soportes de vigas
Las fuerzas cortantes y los momentos flectores a lo largo de una viga no dependen de la geometría de la sección transversal de la viga ni del material del que está hecha la viga. Dependen únicamente de dos factores:
- Cómo se carga la viga.
- Cómo se apoya la viga.
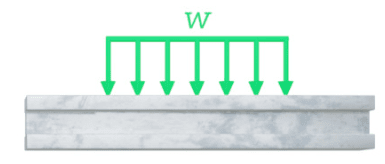
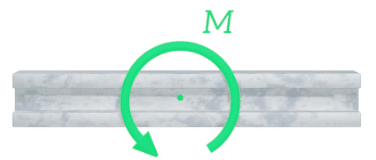
Veamos muchas cosas primero. Las formas más comunes de aplicar cargas a una viga son cargas puntuales, cargas distribuidas y momentos. Las fuerzas distribuidas pueden ser uniformes o no uniformes.

En el mundo real, las vigas se pueden soportar de muchas maneras diferentes, pero para fines de análisis, los soportes reales se pueden modelar como uno de tres soportes idealizados: Soportes fijos, Soportes móviles y Soportes empotrados. Cada uno de estos soportes restringe la viga de diferentes maneras.
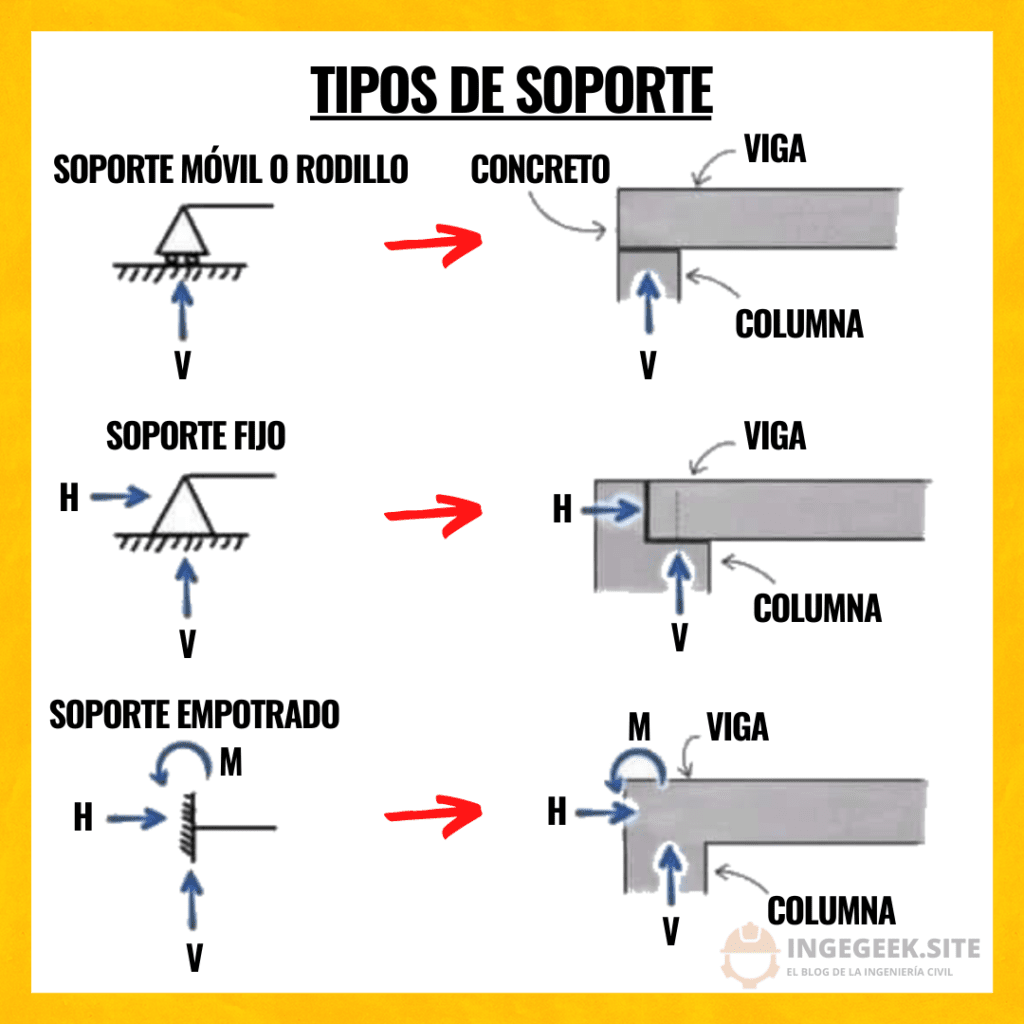
Cuando un cierto grado de libertad (rotación o traslación) está restringido en un soporte, habrá una fuerza o momento de reacción correspondiente en ese lugar. En un soporte fijo, por ejemplo, una viga experimentará fuerzas de reacción horizontales y verticales, porque los desplazamientos horizontales y verticales están restringidos, pero no habrá momento de reacción porque la viga puede girar en el soporte articulado.
Un diagrama de cuerpo libre es un boceto simple que muestra todas las cargas externas que actúan sobre una viga y cualquier fuerza de reacción de los soportes. Averiguar el diagrama de cuerpo libre es un primer paso importante para determinar los diagramas de fuerza cortante y momento flector.
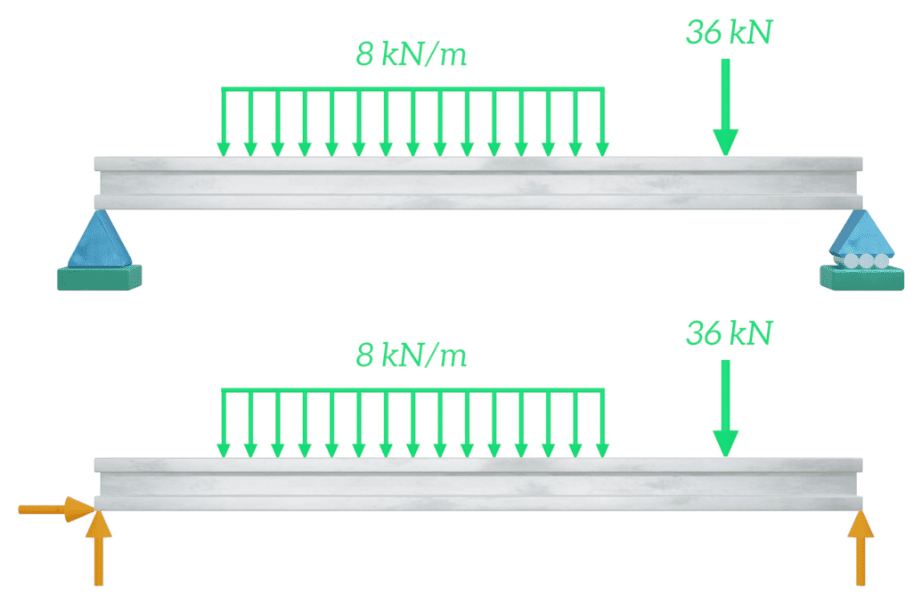
Considere el soporte con pasadores en la configuración de viga que se muestra arriba. La viga puede girar en este soporte, por lo que no hay momento de reacción, pero se evitan los desplazamientos en las direcciones vertical y horizontal, por lo que habrá fuerzas de reacción horizontales y verticales. En el soporte de rodillos sólo existe una fuerza de reacción vertical. Estas tres fuerzas de reacción y las fuerzas concentradas y distribuidas aplicadas se muestran en el diagrama de cuerpo libre.
¿Cómo dibujar el diagrama de fuerza cortante y momento flector?
Hay tres pasos principales que deben seguirse para determinar los diagramas de fuerza cortante y momento flector:
PASO 1: DIBUJE UN DIAGRAMA DE CUERPO LIBRE DE LA VIGA.
Para determinar correctamente las fuerzas cortantes y los momentos flectores a lo largo de una viga, necesitamos conocer todas las cargas que actúan sobre ella, lo que incluye cargas externas y cargas de reacción en los apoyos. Al dibujar el diagrama de cuerpo libre, identifica todas estas cargas y las muestras en un boceto.
PASO 2: CALCULE LAS FUERZAS DE REACCIÓN Y LOS MOMENTOS DE REACCIÓN EN LOS SOPORTES DE LA VIGA.
Aunque las cargas externas se conocen, las fuerzas de reacción y los momentos en los apoyos no; por lo que son necesarios calcularlos. Esto se puede hacer considerando el hecho de que todas las cargas externas, tanto las aplicadas como las cargas en los soportes, deben equilibrarse entre sí. Si no lo hicieran, la viga no estaría en equilibrio estático.
Esto se puede representar mediante tres ecuaciones de equilibrio. Estas ecuaciones establecen que la suma de las fuerzas en la dirección horizontal, la suma de las fuerzas en la dirección vertical y la suma de los momentos tomados respecto de cualquier punto deben ser todas iguales a cero.
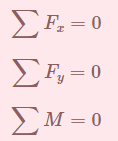
Las fuerzas de reacción y los momentos en los apoyos se pueden calcular utilizando estas ecuaciones.
PASO 3: DETERMINE LAS FUERZAS CORTANTES INTERNAS Y LOS MOMENTOS FLECTORES EN CADA UBICACIÓN A LO LARGO DE LA VIGA.
Ahora tenemos toda la información necesaria para determinar los diagramas de fuerza cortante y momento flector.
Como se mencionó en una parte anterior de este artículo, si hacemos un corte imaginario a través de la viga en cualquier lugar, las fuerzas y momentos internos que actúan sobre la sección transversal cortada deben equilibrar las fuerzas y momentos externos. Esto significa que podemos aplicar una vez más las ecuaciones de equilibrio para calcular las fuerzas cortantes y los momentos flectores a lo largo de la viga.

Comience en un extremo de la viga y mueva la ubicación del corte imaginario al otro extremo, aplicando las ecuaciones de equilibrio y calculando las fuerzas cortantes y los momentos flexionantes a medida que avanza a lo largo de la viga.
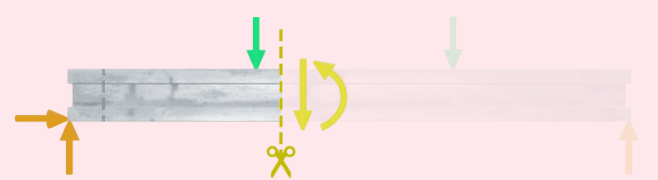
Hacer esto a lo largo de toda la viga le dará los diagramas de fuerza cortante y momento flector.
Convenciones de signos
Es necesario utilizar una convención de signos coherente al calcular las fuerzas cortantes y los momentos flectores. La convención de signos más común es la siguiente:
- Las fuerzas aplicadas son positivas si actúan hacia abajo.
- Si la viga está en el lado izquierdo del plano de corte imaginario, las fuerzas de corte que apuntan hacia abajo son positivas. Si la viga está en el lado derecho del plano de corte, las fuerzas cortantes que apuntan hacia arriba son positivas.
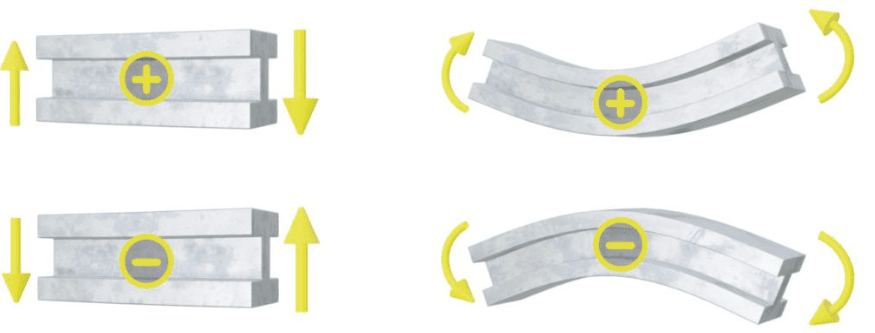
- Si un momento flector provoca hundimiento, entonces es positivo, y si provoca acaparamiento, entonces es negativo.
Estas convenciones de signos se resumen en la siguiente figura.
Ejemplo: viga simplemente apoyada
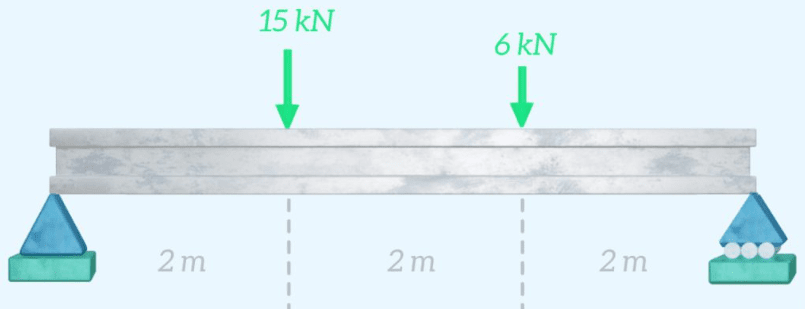
En este ejemplo, determinaremos el diagrama de fuerza cortante y momento flector para una viga simplemente apoyada que soporta dos cargas.
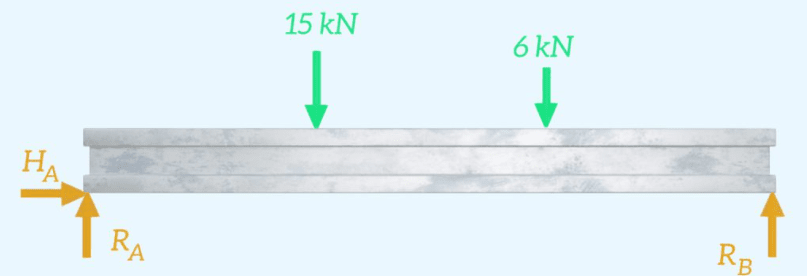
El primer paso es dibujar el diagrama de cuerpo libre. Hay fuerzas de reacción horizontales y verticales en el soporte con pasador (Punto A) y hay una fuerza de reacción vertical en el soporte del rodillo (Punto B).
A continuación, debemos aplicar las ecuaciones de equilibrio para determinar las fuerzas de reacción desconocidas en el punto A y el punto B. La suma de las fuerzas en la dirección horizontal debe ser cero. Ha es la única fuerza en la dirección horizontal, por lo que debe ser igual a cero:
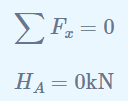
La suma de las fuerzas en dirección vertical debe ser igual a cero:
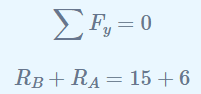
Y la suma de los momentos respecto de cualquier punto debe ser igual a cero. Si elegimos tomar los momentos sobre el Punto B obtenemos lo siguiente:
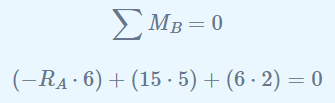
Podemos resolver esta ecuación para determinar que:
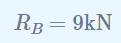
Sustituyendo Rb en la ecuación de equilibrio vertical se obtiene:
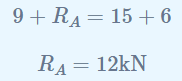
Ahora se han determinado todas las cargas externas que actúan sobre la viga y se puede actualizar el diagrama de cuerpo libre.
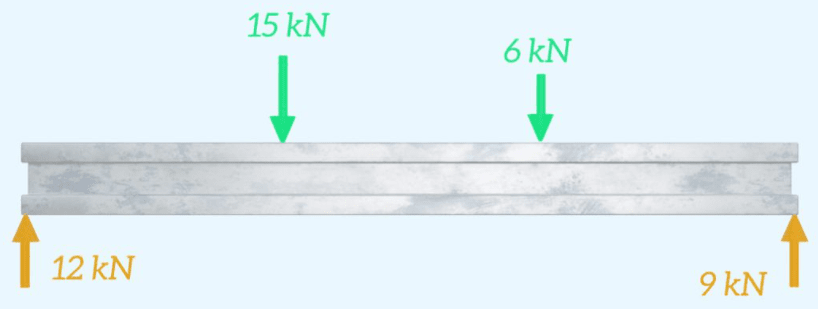
Ahora podemos comenzar a dibujar los diagramas de fuerza cortante y momento flector, comenzando desde el lado izquierdo de la viga. Podemos dibujar el diagrama de cuerpo libre que muestra un segmento de viga que se ha cortado inmediatamente a la derecha de la fuerza de reacción de 12 kN en el punto A.

Para mantener el equilibrio, la fuerza cortante V(x) debe equilibrar la fuerza de reacción de 12 kN:
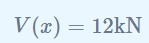
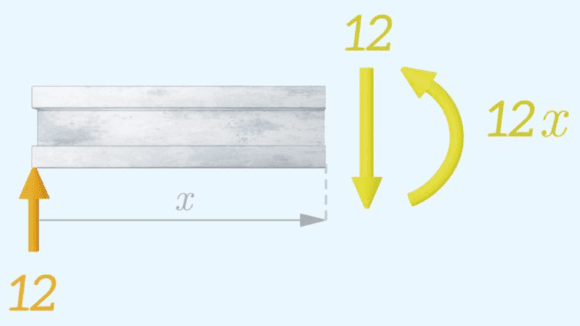
De manera similar, el momento flector debe equilibrar el momento generado por la carga de reacción de 12 kN:

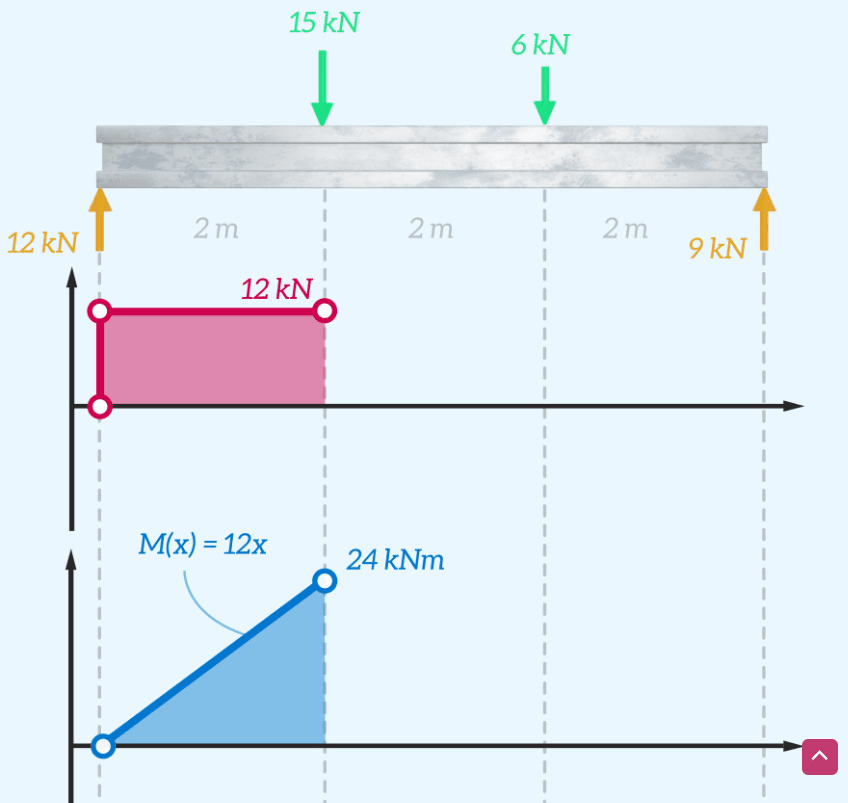
La fuerza cortante será constante hasta que alcancemos la siguiente fuerza aplicada, por lo que podemos dibujarla en el diagrama de fuerza cortante. Y la ecuación obtenida para M(x) es la ecuación de una línea recta, que se puede dibujar en el diagrama de momento flector.
Luego se repite el proceso, moviendo la ubicación del corte imaginario más hacia la derecha. Esta vez el corte se coloca inmediatamente después de la fuerza de 15 kN y se dibuja el diagrama de cuerpo libre. La fuerza cortante y el momento flector se pueden calcular aplicando las ecuaciones de equilibrio.
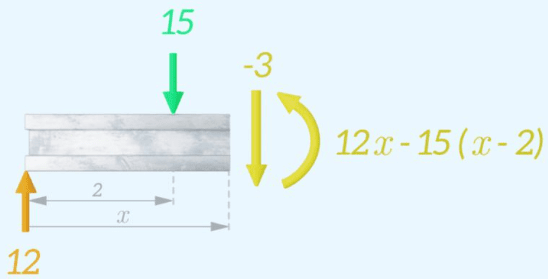
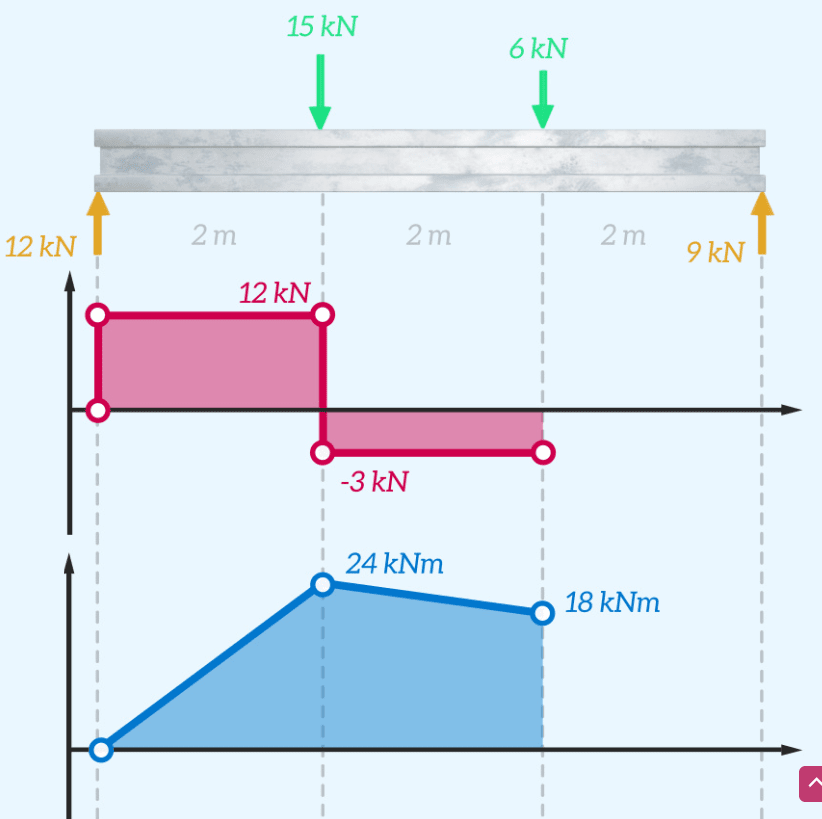
Los diagramas de fuerza cortante y momento flector se pueden actualizar.
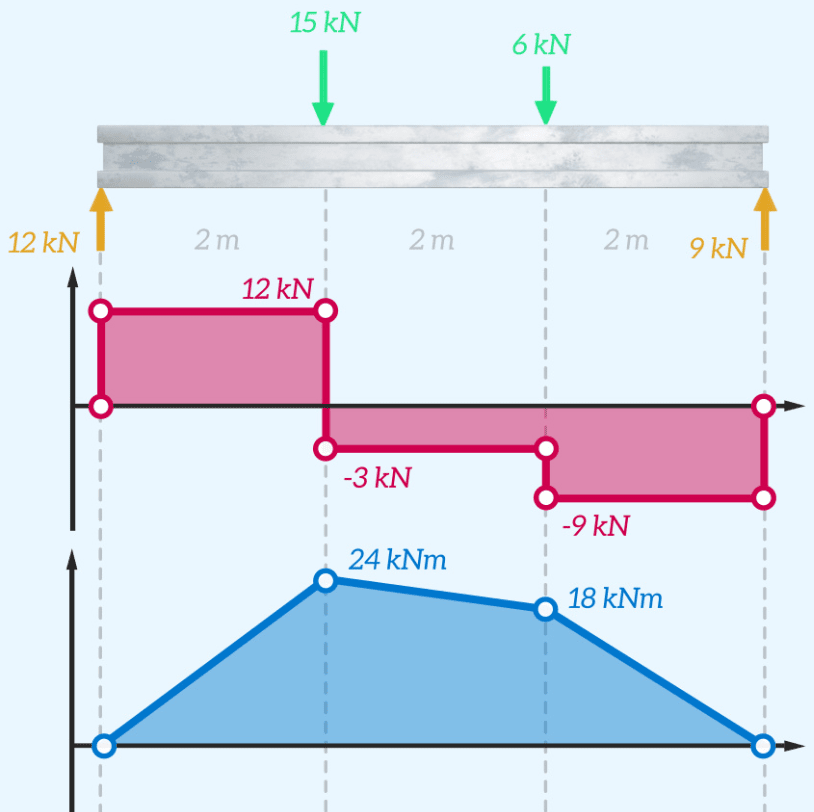
Este proceso se repite hasta cubrir toda la longitud de la viga. Los diagramas completos se muestran a continuación.
🔧 ¿Quieres profundizar en la ingeniería? Descubre «El Glosario del Ingeniero» 📘
Si estás buscando ampliar tus conocimientos en el mundo de la ingeniería, ¡nuestro E-Book «El Glosario del Ingeniero» es tu aliado perfecto! Con una colección exhaustiva de conceptos, definiciones y ejemplos, este libro electrónico te llevará a un viaje de aprendizaje inigualable.



